Ir al contenido principal

LEY COSENO

LEY COSENO

La ley de los cosenos es usada para encontrar las partes faltantes de un triángulo oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluído son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas. En cualquiera de estos casos, es imposible usar la ley de los senos porque no podemos establecer una proporción que pueda resolverse.
La ley de los cosenos establece:
  c 2 = a 2 + b 2 – (2 ab) cos C .
Esto se parece al teorema de Pitágoras excepto que para el tercer término y si C es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras. Así, el teorema de Pitágoras es un caso especial de la ley de los cosenos.
La ley de los cosenos también puede establecerse como
 b 2 = a 2 + c 2 – 2 ac cos B or
 a 2 = b 2 + c 2 – 2 bc cos A .
Ejemplo 1: Dos lados y el ángulo incluido-LAL
Dado a = 11, b = 5 y C = 20°. Encuentre el lado y ángulos faltantes.

    
  Para encontrar los ángulos faltantes, ahora es más fácil usar la ley de los senos.
    

Ejemplo 2: Tres lados incluidos-LLL
Dado a = 8, b = 19 y c = 14.  Encuentre las medidas de los ángulos.
  
  Es mejor encontrar el ángulo opuesto al lado más grande primero. En este caso, ese es el lado b.
    
  Ya que el cos B es negativo, sabemos que B es un ángulo obtuso.
  B ≈ 116.80°
  Ya que B es un ángulo obtuso y un triángulo tiene a lo más un ángulo obtuso, sabemos que el ángulo A y el ángulo C ambos son agudos.
  Para encontrar los otros dos ángulos, es más sencillo usar la ley de los senos. 
   


Ejemplo 3:

 En el siguiente triángulo ABC, a = 13 cm, c = 19cm, <B = 55° , Resuelva el triángulo

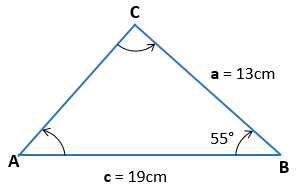
Solución: 
Para poder resolver el siguiente ejercicio, asumimos que el lado que deseamos encontrar es el lado b, puesto que el ángulo opuesto es B, entonces nuestra fórmula queda:
\displaystyle {{b}^{2}}={{a}^{2}}+{{c}^{2}}-2ac\cdot \cos B
De esto resulta
\displaystyle {{b}^{2}}={{13}^{2}}+{{19}^{2}}-2(13)(19)\cdot \cos (55{}^\circ )
\displaystyle {{b}^{2}}=169+361-494(0.5735)
Por lo que:
\displaystyle {{b}^{2}}=246.6532
\displaystyle b=15.7052cm
Ahora tenemos los tres lados de nuestro triángulo, pero nos hace falta conocer los ángulos, para ello, considero un ángulo que deseo calcular que bien puede ser el ángulo A o el ángulo C.
En este caso, elegiré el ángulo A, por lo que mi ecuación quedará:
\displaystyle {{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cdot \cos A
Sin embargo, el valor del lado a, b y c ya los tengo, entonces procedo a despejar el coseno de A, para resolver.
\displaystyle {{a}^{2}}-{{b}^{2}}-{{c}^{2}}=-2bc\cdot \cos A
Despejando aún más…
\displaystyle \frac{{{a}^{2}}-{{b}^{2}}-{{c}^{2}}}{-2bc}=\cos A
Invirtiendo la ecuación
\displaystyle \cos A=\frac{{{a}^{2}}-{{b}^{2}}-{{c}^{2}}}{-2bc}
Listo, ahora es momento de sustituir nuestros valores:
\displaystyle \cos A=\frac{{{13}^{2}}-{{15.7052}^{2}}-{{19}^{2}}}{-2(15.7052)(19)}=0.7350
Ahora aplicando coseno inverso.
\displaystyle A={{\cos }^{-1}}(0.7350)=42.69{}^\circ
Por lo que el ángulo A, es de 42.69 grados.
Ahora mediante la suma de ángulos internos en un triángulo, aplicamos la propiedad para encontrar el ángulo restante:
\displaystyle \angle A+\angle B+\angle C=180{}^\circ
\displaystyle 42.69{}^\circ +55{}^\circ +\angle C=180{}^\circ
Despejando a <C
\displaystyle \angle C=180{}^\circ -42.69{}^\circ +55{}^\circ =82.31{}^\circ
Por lo que nuestro ejercicio está resuelto. Tenemos el triángulo completo 
Aplicación de La Ley Coseno 
1º Un ingeniero topógrafo que se le olvidó llevar su equipo de medición, desea calcular la distancia entre dos edificios. El ingeniero se encuentra en el punto A, y con los únicos datos que tiene hasta ahora son las distancias de el respecto a los otros edificios, 180 m y 210 m, respectivamente, también sabe que el ángulo formado por los dos edificios y su posición actual “A” es de 39.4° ¿Qué distancia hay entre los dos edificios?  
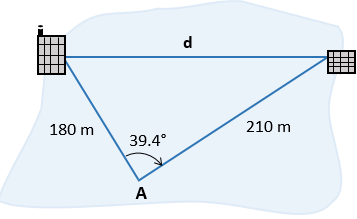
Solución:
Para este caso es importante analizar que tipos de datos tenemos al comienzo, y leyendo el enunciado del problema, así como viendo la imagen podemos darnos cuenta que solamente tenemos dos lados y un ángulo entre dichos lados, es lógico que lo primero que tenemos que hacer, será utilizar la ley de Cosenos.
En este ejercicio vemos que el ángulo que tenemos como dato, es opuesto a la distancia que deseamos encontrar, por lo que nuestra fórmula es ideal para aplicarla de comienzo.
\displaystyle {{d}^{2}}={{(180m)}^{2}}+{{(210m)}^{2}}-2(180m)(210m)\cos (39.4{}^\circ )
despejando el cuadrado del primer miembro:
\displaystyle d=\sqrt{{{(180m)}^{2}}+{{(210m)}^{2}}-2(180m)(210m)\cos (39.4{}^\circ )}
Empezamos a resolver:
\displaystyle d=\sqrt{18081.34{{m}^{2}}}
\displaystyle d=134.47m
Por lo que la distancia entre los dos edificios es de 134.47 metros aproximadamente. 😀
Ahora veamos un ejercicio para aplicar la Ley de Senos.

 2º La distancia entre 2 puntos A y B es de 20 km. Los ángulos de elevación de un globo con respecto a dichos puntos son de 58°20′ y 67°32′. ¿A qué altura del suelo se encuentran?

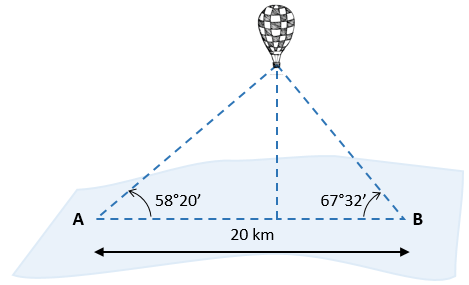
Solución: Podría tratarse de un problema, sumamente complicado… Pero, no lo es. Por lo tanto procedemos a aplicar la ley de senos… No sin antes,  convertir nuestros grados – minutos a grados decimales.
<A = 58°20′ = 58.3333
<B =67°32′ = 67.5333
Comprobamos el ángulo faltante.
\displaystyle \angle A+\angle B+\angle C=180{}^\circ
\displaystyle \angle C=180{}^\circ -\angle A-\angle B
Sustituyendo valores
\displaystyle \angle C=180{}^\circ -58.33{}^\circ -67.53{}^\circ =54.14{}^\circ
Ahora, tenemos los 3 ángulos completos.
Vamos a calcular el lado a, que sería el lado opuesto al ángulo A 
No podríamos aplicar la ley de cosenos, porque nos haría falta un lado forzosamente, por lo tanto recurrimos aplicar la ley de senos.
\displaystyle \frac{a}{senA}=\frac{b}{senB}=\frac{c}{senC}
Tenemos los 20Km que el problema nos da de referencia, y tenemos el ángulo opuesto a ese lado, que es el que encontramos de 54.14°, entonces tomamos esos datos para aplicar la ley de senos, a cualquier otro lado.
\displaystyle \frac{a}{senA}=\frac{c}{senC}
Despejando “a”
\displaystyle a=\frac{c\cdot senA}{senC}
Sustituyendo valores:
\displaystyle a=\frac{20km\cdot sen(58.33{}^\circ )}{sen(54.14{}^\circ )}=21km
Por lo que, el lado a mide 21 kilómetros.
Ahora podemos aplicar la función seno del ángulo 67.53 para obtener el cateto opuesto, que sería nuestra altura.
\displaystyle sen67.53{}^\circ =\frac{h}{20.95km}
despejando h = altura del globo
\displaystyle h=(sen67.53)(21km)=19.40km
Por lo que la altura del globo, es de 19.4 kilómetros aproximadamente (Redondeando).

Comentarios

  1. Unknown4 de julio de 2021, 11:56 a.m.

    Hola gracias por los problemas y la explicación, me gustaría saber porque en el ejercicio tres del globo luego de hallar los ángulos y usar la ley de senos para calcular el otro lado porque la altura se puede calcular a través de la función seno, es decir porque se toma el valor de la distancia completa de 21 km aproximados y no una distancia menor al asumir que se esta calculando es desde la mitad de esa distancia más o menos y no la distancia completa , no se si me explico, pienso que esa distancia es más pequeña ahora para poder hallar la altura y no es 21 Km , me gustaría por favor me explicará porque se toma completa esa distancia , porque se asume que es toda ?????
    Gracias.

    ResponderBorrar

Publicar un comentario

Entradas más populares de este blog

SISTEMA CICLICO

SISTEMA  CÍCLICO En el sistema cíclico el ángulo unidad es el radian (rad) que es un ángulo con vértice en el centro de una circunferencia y cuyos lados abarcan un arco de longitud igual al radio de la circunferencia Se establece que 360°=2π rad. Por lo tanto 1 vuelta (360°)= 2π rad  .5 vuelta (180°) = π rad DE SISTEMA CÍCLICO A GRADOS Y VICEVERSA Se pueden realizar mediante regla de 3 basándonos siempre en que 180° es equivalente a π rad.                    
Publicar un comentario
Leer más

Funcion Cubica

 Funcion Cubica Una función cúbica (o función de tercer grado) es una función polinómica de grado 3, es decir, que el mayor exponente del polinomio es x elevado a 3 (x3): La representación gráfica de la función cúbica es: Una función cúbica puede tener tres, dos o una raíz. Las raíces de una función son los elementos del dominio tal que su imagen es nula (f(x) = 0). Caracteristicas de la funcion cubica Siendo f(x) = ax3+bx2+cx+d, entonces tenemos que: Dominio: R. Codominio: R
Publicar un comentario
Leer más