Ir al contenido principal

ÁNGULOS COMPLEMENTARIOS Y SUPLEMENTARIOS

Ángulos Complementarios

Los ángulos complementarios son dos ángulos cuyas medidas suman 90 o .
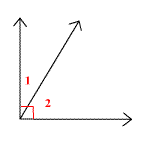
En la siguiente figura,  1 y  2 son complementarios.
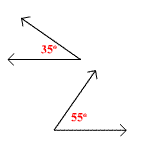
Dos ángulos no necesitan ser adyacentes para ser complementarios. Los ángulos en la siguiente figura también son complementarios, ya que 35 o + 55 o = 90 o .

Ángulos suplementarios

Los ángulos suplementarios son dos ángulos cuyas medidas suman 180 o .
Los dos ángulos de una pareja lineal , como 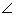 1 y 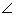 2 en la siguiente figura, son siempre suplementarios.
Pero, dos ángulos no necesitan ser adyacentes para ser suplementarios. En la siguiente figura, 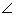 3 y 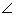 4 son suplementarios, porque sus medidas suman 180 o .
Ejemplo 1:
Dos ángulos son suplementarios. Si la medida del ángulo es dos veces la medida del otro, encuentre la medida de cada ángulo.
Digamos que la medida de uno de los ángulos suplementarios sea a .
La medida del otro ángulo es 2 por a .
Así, la medida del otro ángulo es 2 a .
Si la suma de las medidas de dos ángulos es 180°, entonces los ángulos son suplementarios.
Así, a + 2 a = 180°
Simplifique.
3 a = 180°
Para aislar a , divida ambos lados de la ecuación entre 3.
La medida del segundo ángulo es,
Así, las medidas de los dos ángulos suplementarios son 60° y 120°.

Ejemplo 2:
Encuentre  si  son suplementarios,  , y  .
La suma de las medidas de dos ángulos suplementarios es 180°.
Así, 
Sustituya  por  y  por  .
Combine los términos semejantes. Obtenemos:
Sume 23 en ambos lados. Obtenemos:
Divida ambos lados entre 7.
Simplifique.
Para encontrar  , sustituya 29 por x en  .
Simplifique.
58 + 15 = 73
Así,  .
Para encontrar  , sustituya 29 por x en  .
Simplifique.
Así,  .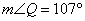

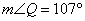Comentarios

Publicar un comentario

Entradas más populares de este blog

LEY COSENO

LEY COSENO La  ley de los cosenos  es usada para encontrar las partes faltantes de un triángulo oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluído son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas. En cualquiera de estos casos, es imposible usar la ley de los senos porque no podemos establecer una proporción que pueda resolverse. La ley de los cosenos establece:    c  2  =  a  2  +  b  2  – (2  ab)  cos  C  . Esto se parece al teorema de Pitágoras excepto que para el tercer término y si  C  es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras. Así, el teorema de Pitágoras es un caso especial de la ley de los cosenos. La ley de los cosenos también puede establecerse como  b  2  =  a  2  +  c...
1 comentario
Leer más

SISTEMA CICLICO

SISTEMA  CÍCLICO En el sistema cíclico el ángulo unidad es el radian (rad) que es un ángulo con vértice en el centro de una circunferencia y cuyos lados abarcan un arco de longitud igual al radio de la circunferencia Se establece que 360°=2π rad. Por lo tanto 1 vuelta (360°)= 2π rad  .5 vuelta (180°) = π rad DE SISTEMA CÍCLICO A GRADOS Y VICEVERSA Se pueden realizar mediante regla de 3 basándonos siempre en que 180° es equivalente a π rad.                    
Publicar un comentario
Leer más

Funcion Cubica

 Funcion Cubica Una función cúbica (o función de tercer grado) es una función polinómica de grado 3, es decir, que el mayor exponente del polinomio es x elevado a 3 (x3): La representación gráfica de la función cúbica es: Una función cúbica puede tener tres, dos o una raíz. Las raíces de una función son los elementos del dominio tal que su imagen es nula (f(x) = 0). Caracteristicas de la funcion cubica Siendo f(x) = ax3+bx2+cx+d, entonces tenemos que: Dominio: R. Codominio: R
Publicar un comentario
Leer más