OPERACIONES CON FRACCIONES
En esta página explicamos las operaciones entre fracciones (suma, resta, multiplicación y división) y resolvemos 10 problemas. Es necesario que sepáis calcular el mínimo común múltiplo y el máximo común divisor.
Índice:
- Conceptos necesarios
- Suma y resta de fracciones con denominador común
- Suma y resta de fracciones con distinto denominador
- Multiplicación de fracciones
- División de fracciones
- Fracción de un número
- Más problemas
1. Conceptos necesarios
Dada una fracción ,
- es el numerador
- es el denominador
Si dividimos un todo en partes iguales, la fracción son de estas partes:
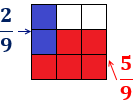
Fracción irreductible
La fracción es irreductible si el máximo común divisor de y es 1. Esto significa que el resultado de la división es un número decimal.
Si una fracción no es irreductible, podemos transformarla en una fracción irreductible dividiendo el numerador y el denominador entre su máximo común divisor.
Otro método para simplificar es escribir numerador y denominador como productos para eliminar los factores comunes.
Más información y ejemplos de fracciones irreductibles en fracción irreductible.
2. Suma y resta de fracciones con denominador común suma
Cuando dos fracciones tienen el mismo denominador, su suma se calcula sumando los numeradores:
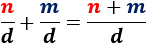
¡Los denominadores no se suman!
La suma de (cinco novenos) y (dos novenos) son (siete novenos):
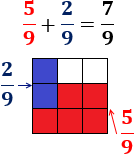
Resta:
La resta de dos fracciones con denominador común se calcula restando sus numeradores:
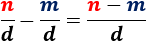
La resta de (cinco novenos) menos (dos novenos) es (un tercio):
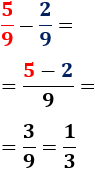
En el último paso hemos dividido numerador y denominador entre 3.
Problema 1
Calcular las siguientes sumas de fracciones con denominador común:

Solución
Como tienen denominador común, sólo hay que sumar los numeradores y simplificar el resultado:
Problema 2
Calcular las siguientes restas de fracciones con denominador común:
Solución
Como tienen denominador común, sólo hay que restar los numeradores y simplificar el resultado:
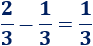
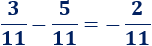
- Observa que la fracción es negativa (se conserva el signo de la fracción mayor).
3. Suma y resta de fracciones con distinto denominador
Suma:
Si los denominadores son distintos, la suma no se calcula simplemente sumando sus denominadores. Por ejemplo, consideremos las fracciones y :
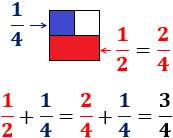
La fracción es igual a la fracción (se observa perfectamente en la representación). Si usamos esta fracción en lugar de , tenemos denominador común y podemos sumar las fracciones fácilmente.
Luego, lo que tenemos que hacer es cambiar una o ambas fracciones por fracciones equivalentes de forma que ambas tengan el
Método
Para hacer esto, escribiremos como nuevo denominador al mínimo común múltiplo de los dos denominadores:
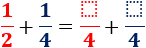
Los numeradores se calculan dividiendo el nuevo denominador entre el antiguo y multiplicando el resultado por el antiguo numerador:

Resta:
Para calcular la resta, procedemos del mismo modo, pero restando los numeradores en el paso final.
Problema 3
Calcular las siguientes sumas de fracciones con denominador distinto:
Solución
El mínimo común múltiplo de y es . Por tanto, tenemos
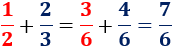
El mínimo común múltiplo de y es . Por tanto, tenemos
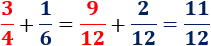
El mínimo común múltiplo de y es . Por tanto, tenemos
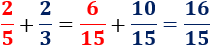
Problema 4
Calcular las siguientes restas de fracciones con denominador distinto:
Solución
El mínimo común múltiplo de y es . Por tanto, tenemos
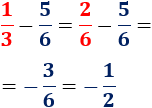
El mínimo común múltiplo de y es . Por tanto, tenemos
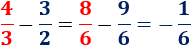
El mínimo común múltiplo de y es . Por tanto, tenemos
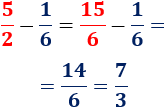
4. Multiplicación de fracciones
La multiplicación de fracciones es muy fácil de calcular y no importa si tienen denominador común o no:
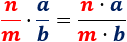
Es decir, se multiplican los numeradores y los denominadores.
Por ejemplo,
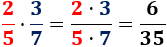
5. División de fracciones
La división de fracción se calcula multiplicando numerador y denominador en cruz:
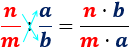
Por ejemplo,
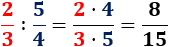
Es decir,
- El numerador es el producto del numerador de la primera fracción y del denominador de la segunda.
- El denominador es el producto del denominador de la primera fracción y del numerador de la segunda.
También, podemos escribir la división como
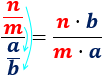
Regla que suele ayudar: el de arriba () por el de abajo () entre los dos del medio ( y ).
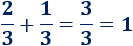
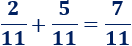
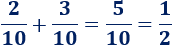
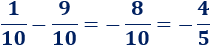
Comentarios
Publicar un comentario