PROBLEMAS DE TRIGONOMÉTRICA BÁSICA

PROBLEMAS DE TRIGONOMÉTRICA BÁSICA

(Seno, Coseno y Tangente)

En esta página definimos las razones trigonométricas seno, coseno y tangente de un ángulo como la razón entre los lados de un triángulo rectángulo. También, resolvemos 10 problemas de aplicación.

Introducción

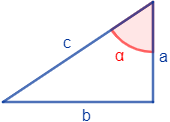
Consideremos un triángulo rectángulo (con un ángulo recto) y un ángulo $\alpha$:

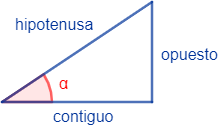
El lado opuesto al ángulo recto (el de 90º) se denomina hipotenusa y los otros dos lados son los catetos:

• el cateto opuesto es el que está enfrente del ángulo $\alpha$
• y el cateto contiguo o adyacente es el otro cateto, es decir, el que está en contacto con el ángulo $\alpha$.

Las razones trigonométricas se definen como la razón entre los lados del triángulo:

Seno

El seno de $\alpha$ es el cateto opuesto entre la hipotenusa:

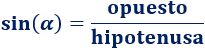
Coseno

El coseno de $\alpha$ es el cateto contiguo o adyacente entre la hipotenusa:

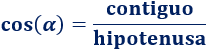
Tangente

La tangente de $\alpha$ es seno entre el coseno, es decir, el cateto opuesto entre el contiguo:

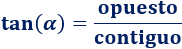
Otra forma de escribir la tangente de $\alpha$ es $tg\left(\alpha \right)$.

Nota: tened en cuenta que, si cambiamos de ángulo, entonces cambian los catetos: el opuesto pasa a ser el contiguo y viceversa.

Una regla mnemotecnia que puede ayudaros a recordar las fórmulas:

• Seno - opuesto
• Coseno - contiguo
• Tangente = seno/coseno = opuesto/contiguo

Finalmente, veamos por encima qué son las razones trigonométricas inversas

Razones inversas

Si conocemos el seno, el coseno o la tangente del ángulo $\alpha$ y queremos calcular el ángulo $\alpha$, usamos las razones trigonométricas inversas:

º La inversa del seno es el arcoseno, escrita como $arc\mathrm{os}in$:

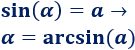
En la calculadora es la tecla $si{n}^{-1}$.

º La inversa del coseno es el arcocoseno, escrita como 

$arccos$:

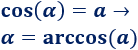
En la calculadora es la tecla $co{s}^{-1}$.

º La inversa de la tangente es la arcotangente, escrita como arcotan:

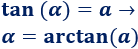
En la calculadora es la tecla $ta{n}^{-1}$.

Problemas resueltos de trigonometría

Problema 1

Determinar si los lados $a$, $b$ y $c$ de cada uno de los siguientes triángulos rectángulos son la hipotenusa, el lado opuesto o el lado contiguo al ángulo $\alpha$ representado:

Triángulo 1:

Triángulo 2:

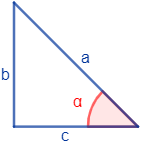
Triángulo 3:

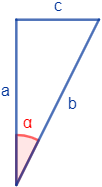
Triángulo 1:

• $a$ es el lado contiguo o adyacente
• $b$ es el lado opuesto
• $c$ es la hipotenusa

Triángulo 2:

• $a$ es la hipotenusa
• $b$ es el lado opuesto
• $c$ es el lado contiguo o adyacente

Triángulo 3:

• $a$ es el lado contiguo o adyacente
• $b$ es la hipotenusa
• $c$ es el lado opuesto

Problema 2

(Con calculadora) Calcular los ángulos $\alpha$ sabiendo cuánto valen su seno o su coseno:

a) $sin\left(\alpha \right)=0.999390827$

b) $sin\left(\alpha \right)=0.6691306064$

c) $sin\left(\alpha \right)=0.7660444431$

d) $sin\left(\alpha \right)=0.9743700648$

e) $cos\left(\alpha \right)=0.8090169944$

f) $cos\left(\alpha \right)=0.2588190451$

g) $cos\left(\alpha \right)=0.9271838546$

h) $cos\left(\alpha \right)=0.4067366431$

Para calcular el ángulo utilizamos la función arcoseno $arcsin$ (en la calculadora es $si{n}^{-1}$) ó
arcocoseno
$arccos$ (en la calculadora es $co{s}^{-1}$).


a)



b)



c)



d)



e)



f)



g)



h)

Problema 3

Calcular el valor de x de cada figura utilizando las razones trigonométricas vistas:

$x$

Figura 1:

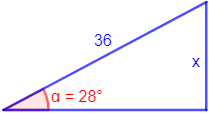
Figura 2:

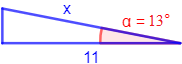
Figura 3:

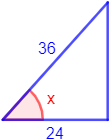
Figura 4:

Conocemos la hipotenusa y el ángulo. Como queremos calcular el lado opuesto,

 utilizamos el seno:

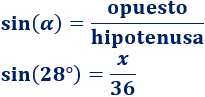
Despejamos la incógnita:

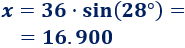
El lado mide, aproximadamente, 16.900.

figura 2:

En esta figura conocemos el lado contiguo y el ángulo. Para calcular la hipotenusa,

utilizamos el coseno:

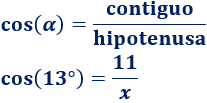
Despejamos la incógnita:

La hipotenusa mide, aproximadamente, 11.289.

Figura 3:

Conocemos el lado contiguo y la hipotenusa, así que utilizamos el coseno:

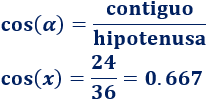
Despejamos la incógnita:

Por tanto, el ángulo mide, aproximadamente, 48.164°.

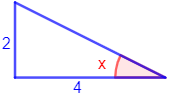
Figura 4:

Como conocemos el lado opuesto y el contiguo al ángulo, utilizamos la tangente:

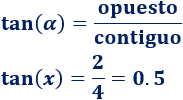
Despejamos la incógnita:

Por tanto, el ángulo mide, aproximadamente, 26.565°.