El teorema de Pitágoras
El teorema de Pitágoras fue nombrado así en honor de Pitágoras de Samos , un matemático que también fue un lider religioso, y creyó que todas las cosas en el universo estaban compuestas de números.
Se supone que él ha sido el primero en probar este teorema acerca de los triángulos rectángulos:
Teorema de Pitágoras . En un triángulo rectángulo con catetos de longitudes a y b e hipotenusa de longitud c , la ecuación siguiente es verdadera:
c 2 = a 2 + b 2
(Hay muchas formas diferentes de probar esto.)
La hipotenusa de un triángulo rectángulo es el lado opuesto al ángulo recto.
A continuación está una representación gráfica. El teorema establece que la suma de las áreas de los cuadrados azul y rojo es igual al área del cuadrado verde.
Importante : Recuerde que el teorema de Pitágoras es verdadero solo para triángulos rectángulos – triángulos que tienen un ángulo de 90 o .
La conversa del teorema también es verdadera: si un triángulo tiene lados de longitudes a , b , y c , y c 2 = a 2 + b 2 , entonces debe ser un triángulo rectángulo .
Problema 1
En el siguiente triángulo, ¿cuál de los lados es la hipotenusa y cuál es el ángulo recto?
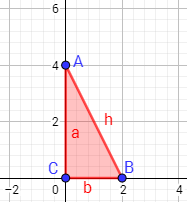

Calcular cuánto mide la hipotenusa.Los catetos son los lados y . La hipotenusa es el lado . El ángulo recto es el ángulo que forman ambos catetos.Para calcular la longitud de la hipotenusa, aplicamos Pitágoras. Los catetos miden y , con lo que:
Finalmente, hacemos la raíz cuadrada:
Simplificamos el resultado escribiendo el radicando como un producto y aplicando la propiedad de que la raíz de una producto es el producto de las raíces de sus factores:
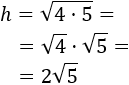
Si aproximamos, h=4,47
Problema 2
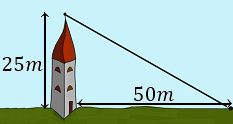
Se quiere colocar un cable desde la cima de una torre de 25 metros altura hasta un punto situado a 50 metros de la base la torre. ¿Cuánto debe medir el cable?
El cable coincide con la hipotenusa de un triángulo rectángulo cuyos catetos miden y .
Calculamos la longitud del cable (es la hipotenusa ):
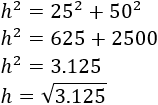
Como , podemos simplificar:
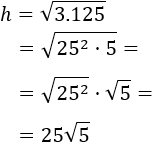
El cable debe medir metros, es decir, aproximadamente 56 metros
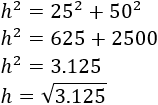
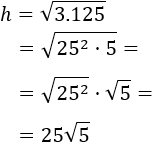
Problema 3
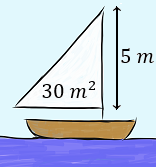
Hallar las medidas de los lados de una vela con forma de triángulo rectángulo si se quiere que tenga un área de 30 metros al cuadrado y que uno de sus catetos mida 5 metros para que se pueda colocar en el mástil.
Llamamos , y a la altura, base e hipotenusa de la vela.
Por un lado, como el área de un triángulo es base por altura, tenemos
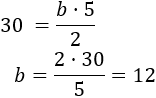
De donde tenemos que la base debe medir 12 metros.
Por otro lado, como la vela tiene forma de triángulo rectángulo, podemos calcular la hipotenusa por Pitágoras:
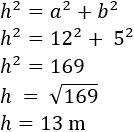
Por tanto, los lados de la vela deben medir 5, 12 y 13 metros

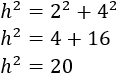
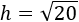
Comentarios
Publicar un comentario