Ir al contenido principal

Dominio y Rango

 

Dominio y rango de una función

El dominio de una función f ( x ) es el conjunto de todos los valores para los cuales la función está definida, y el rango de la función es el conjunto de todos los valores que f toma.

(En gramática, probablemente le llame al dominio el conjunto reemplazo y al rango el conjunto solución. Quizá también estos han sido llamados la entrada y salida de la función.)


Ejemplo 1:

Considere la función mostrada en el diagrama.

Aquí, el dominio es el conjunto { A , B , C , E }. D no está en el dominio, ya que la función no está definida para D .

El rango es el conjunto {1, 3, 4}. 2 no está en el rango, ya que no hay letra en el dominio que se enlace con el 2.

Ejemplo 2:

El dominio de la función

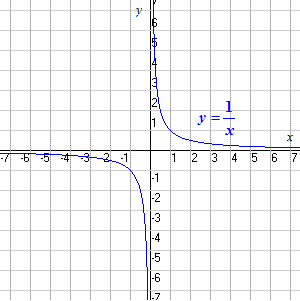
f ( x ) = 1/ x

es todos los números reales excepto el cero (ya que en x = 0, la función no está definida: la división entre cero no está permitida!).

El rango también es todos los números reales excepto el cero. Puede ver que hay algún punto en la curva para cada valor de y excepto para y = 0.


Los dominios pueden también estar explícitamente especificados, si hay valores para los cuales la función pudiera estar definida, pero que no deseamos considerarlos por alguna razón.













Comentarios

Publicar un comentario

Entradas más populares de este blog

LEY COSENO

LEY COSENO La  ley de los cosenos  es usada para encontrar las partes faltantes de un triángulo oblicuo (no rectángulo) cuando ya sea las medidas de dos lados y la medida del ángulo incluído son conocidas (LAL) o las longitudes de los tres lados (LLL) son conocidas. En cualquiera de estos casos, es imposible usar la ley de los senos porque no podemos establecer una proporción que pueda resolverse. La ley de los cosenos establece:    c  2  =  a  2  +  b  2  – (2  ab)  cos  C  . Esto se parece al teorema de Pitágoras excepto que para el tercer término y si  C  es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras. Así, el teorema de Pitágoras es un caso especial de la ley de los cosenos. La ley de los cosenos también puede establecerse como  b  2  =  a  2  +  c  2  – 2  ac  cos  B  or  a  2  =  b  2  +  c  2  – 2  bc  cos  A  . Ejemplo 1:  Dos lados y el ángulo incluido -LAL Dado a = 11, b = 5 y C = 20°. E
1 comentario
Leer más

SISTEMA CICLICO

SISTEMA  CÍCLICO En el sistema cíclico el ángulo unidad es el radian (rad) que es un ángulo con vértice en el centro de una circunferencia y cuyos lados abarcan un arco de longitud igual al radio de la circunferencia Se establece que 360°=2π rad. Por lo tanto 1 vuelta (360°)= 2π rad  .5 vuelta (180°) = π rad DE SISTEMA CÍCLICO A GRADOS Y VICEVERSA Se pueden realizar mediante regla de 3 basándonos siempre en que 180° es equivalente a π rad.                    
Publicar un comentario
Leer más

Funcion Cubica

 Funcion Cubica Una función cúbica (o función de tercer grado) es una función polinómica de grado 3, es decir, que el mayor exponente del polinomio es x elevado a 3 (x3): La representación gráfica de la función cúbica es: Una función cúbica puede tener tres, dos o una raíz. Las raíces de una función son los elementos del dominio tal que su imagen es nula (f(x) = 0). Caracteristicas de la funcion cubica Siendo f(x) = ax3+bx2+cx+d, entonces tenemos que: Dominio: R. Codominio: R
Publicar un comentario
Leer más