Funcion Cuadratica

La forma general de una función cuadrática es f ( x ) = ax 2 + bx + c . La gráfica de una función cuadrática es una parábola , un tipo de curva de 2 dimensiones.

La parábola "básica", y = x 2 , se ve así:

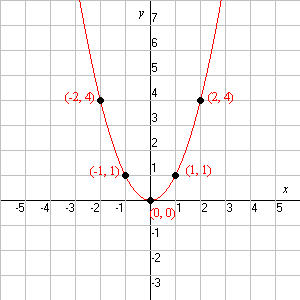
La función del coeficiente a en la ecuación general es de hacer la parábola "más amplia" o "más delgada", o de darle la vuelta (si es negativa):

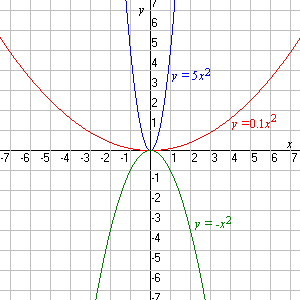
Si el coeficiente de x 2 es positivo, la parábola abre hacia arriba; de otra forma abre hacia abajo.

Una función cuadrática (o función de segundo grado) es una función polinómica de grado 2, es decir, el mayor exponente del polinomio es x elevado a 2 (x2).

Su forma estándar es:

Son a, b y c escalares, valores constantes o denominados, que también se denominan los coeficientes de la función.

Su representación gráfica es una parábola vertical.

Existen dos elementos fundamentales en la parábola que definen como es esta:

1- El eje de simetría, que es una recta vertical que parte la parábola en dos ramas iguales.

2- El vértice: es el punto de intersección de la parábola con el eje de simetría.

Si el escalar a > 0, la parábola se abre hacia arriba y el vértice es el mínimo de la función. En cambio, si a < 0, la parábola se abre hacia abajo y el vértice es el máximo de la función.

Cuanto mayor sea el valor absoluto de a, |a|, más juntas estarán las ramas de la parábola.

Una función cuadrática puede tener dos raíces reales, una o ninguna raíz real (en este caso serán dos raíces imaginarias). Las raíces de una función son los elementos del dominio tal que su imagen es nula (f(x) = 0). Dicho de otra manera, las raíces son los puntos donde la gráfica de la función corta el eje x.

Una ecuación cuadrática o de segundo orden es cuando la función cuadrática se iguala a cero: f(x) = y = 0. Tiene la forma:

La fórmula para el cálculo de las raíces de una ecuación cuadrática es:

Al contenido comprendido dentro del radical de esta fórmula se le llama discriminante y se representa así:

Se puede también expresar la ecuación cuadrática, en función de sus raíces y del escalar a, de esta manera, por factorización:

La ecuación de la recta del eje de simetría, por el mismo concepto de la simetría, se puede hallar con la media aritmética de los puntos de corte con el eje x, es decir, la media aritmética de sus raíces:

Puntos de corte:

Las intersecciones son los puntos en los que la función corta los ejes y y x.

La intersección con el eje y de una función cuadrática se produce cuando hacemos x = 0. Es siempre el punto (0, c). Si la función es incompleta y no existe el parámetro c (es decir, c = 0), la intersección será el punto (0, 0).

La intersección con el eje x de una función cuadrática son las raíces x1 y x2 de la misma.

Se producen cuando hacemos y = 0. Como se ha dicho más arriba y dependiendo del discriminante Δ, pueden haber dos o una raíces reales, o en el caso de que Δ < 0 entonces son raíces complejas.

Dominio y Rango

Siendo f(x) = ax2+bx+c, entonces tenemos que:

• Dominio: Dominio de la función cuadrática.
• Codominio: Codominio de la función cuadrática.
• Derivada de la función cuadrática: Derivada de la función cuadrática.
• Integral de la función cuadrática: