FUNCION TRIGONOMETRICA

las funciones trigonometricas f son aquellas que están asociadas a una razón trigonométrica.

Las razones trigonométricas de un ángulo α son las obtenidas entre los tres lados de un triángulo rectángulo. Es decir, las comparaciones por su cociente de sus tres lados a, b y c.

Existen 6 razones trigonometricas...

Seno

El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la hipotenusa

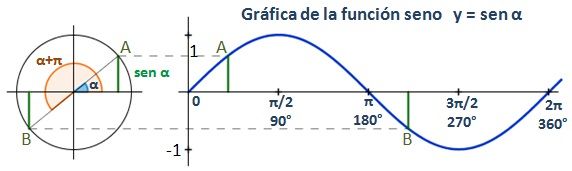
La función del seno es periódica de período 360º (2π radianes), por lo que esta sección de la gráfica se repetirá en los diferentes períodos.

• Dominio: 
• Codominio: 
• Derivada de la función seno: 
• Integral de la función seno: 

Coseno

El coseno de un ángulo α se define como la razón entre el cateto contiguo o cateto adyacente (b) y la hipotenusa (c).

La función del coseno es periódica de período 360º (2π radianes).

• Dominio: 
• Codominio: 
• Derivada de la función coseno: 
• Integral de la función coseno: 

Tangente:

La tangente de un ángulo α es la razón entre el cateto opuesto (a) y el cateto contiguo o cateto adyacente (b).

La función de la tangente es periódica de período 180º (π radianes).

• Dominio:  (excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;…
• Codominio: 
• Derivada de la función tangente: 
• Integral de la función tangente: 

Cosecante

La cosecante es la razón trigonométrica recíproca del seno, es decir csc α · sen α=1.

La cosecante del ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto opuesto (a).

La función de la cosecante es periódica de período 360º (2π radianes).

• Dominio:  (excepto a · π), siendo a un número entero.
• Codominio: 
• Derivada de la función cosecante: 
• Integral de la función cosecante:
  

Secante

La secante es la razón trigonométrica recíproca del coseno, es decir sec α · cos α=1.

La secante de un ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto contiguo o cateto adyacente (b).

Cotangente

La cotangente es la razón trigonométrica recíproca de la tangente, por lo tanto tan α · cot α=1.

La cotangente de un ángulo α de un triángulo rectángulo se define como la razón entre el cateto contiguo o cateto adyacente (b) y el cateto opuesto (a).

La función de la cotangente es periódica de período 180º (π radianes).

• Dominio:  (excepto a · π), siendo a un número entero.
• Codominio: 
• Derivada de la función cotangente:
  
• Integral de la función cotangente: